-
blog.DavidNavara | blog.MartinHabina | blog.VítězslavHouška | blog.RobertCvek | blog.VlastimilChládek | blog.SoňaPertlová | blog.DavidKaňovský | blog.PavelMatocha | blog.VáclavKlaus | blog.JanHofírek | blog.LuděkSedlák | blog.MichalŠpaček | blog.IgorNěmec | blog.VladoHrtko | blog.OtakarVálek | blog.JánMarkoš |


Štěpán Žilka
mezinárodní šachový velmistr (2531)
Logaritmus v praxi aneb šachová kariéra z matematické perspektivy
[25.02.2011 16:07:41]
Pár přátel se mi již ozvalo s dotazem, jestli neplánuji napsat další blog, že prý nemám čekat na další vyhraný Praha open OK, dokud se vám mé blogy líbí, budu psát... Protože se mi občas podaří odehrát excelentní turnaj, ale mé elo je pořád stejné, asi vás napadne, že tyto výsledky musím občas vykompenzovat nějakým šachovým výbuchem. Vás, milující pokoru a skromnost, ale musím zklamat, nebudu dnes psát o tom, jak jsem v Rakousku po haluzi uhrál pouhou půlku a jak jsem tím svému týmu nepomohl k ničemu než k dosažení sestupové příčky před posledním dvojkolem, ani o tom, jak jsem v posledním extraligovém trojkole udělal dvě hrubé chyby. Dnes vám nabídnu náhled na šachovou kariéru jinak, než jak jste o ní asi kdy přemýšleli. Vím, že středoškolská matematika nebude koníčkem většinové populace, ale nebojte se. Ani já ji nijak nehltal. Vždy mě zajímalo pouze to, co jsem dokázal použít v praxi. Takže zatímco jsem písemky z analytické geometrie vyplňoval jako malou násobilku, na integrální počet jsem chodil s tahákama po kapsách. V dalším textu se budu snažit být co nejvíce názorný a matematiku co nejvíce schovat, i když její přítomnost bude vždy dobře cítit.
OK, dokud se vám mé blogy líbí, budu psát... Protože se mi občas podaří odehrát excelentní turnaj, ale mé elo je pořád stejné, asi vás napadne, že tyto výsledky musím občas vykompenzovat nějakým šachovým výbuchem. Vás, milující pokoru a skromnost, ale musím zklamat, nebudu dnes psát o tom, jak jsem v Rakousku po haluzi uhrál pouhou půlku a jak jsem tím svému týmu nepomohl k ničemu než k dosažení sestupové příčky před posledním dvojkolem, ani o tom, jak jsem v posledním extraligovém trojkole udělal dvě hrubé chyby. Dnes vám nabídnu náhled na šachovou kariéru jinak, než jak jste o ní asi kdy přemýšleli. Vím, že středoškolská matematika nebude koníčkem většinové populace, ale nebojte se. Ani já ji nijak nehltal. Vždy mě zajímalo pouze to, co jsem dokázal použít v praxi. Takže zatímco jsem písemky z analytické geometrie vyplňoval jako malou násobilku, na integrální počet jsem chodil s tahákama po kapsách. V dalším textu se budu snažit být co nejvíce názorný a matematiku co nejvíce schovat, i když její přítomnost bude vždy dobře cítit.
Podobnost problémů
Je možné něco tak složitého jako je šachová kariéra vyjádřit jednoduchým matematickým vzorcem? Těžko. Nicméně můžeme vytvořit jednoduchý problém podobný tomu složitému, který bude mít jeho základní vlastnosti a přitom bude snadné ho matematicky popsat a neplavat tak ve zcela neznámém prostředí. A o tom bude můj dnešní blog. Řekneme si, proč je šachový růst podobný logaritmické funkci a hlavně, co z toho vyplývá.
Co je to logaritmus?
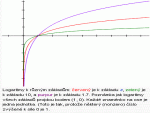
Pro ty, kteří slyší toto slovo poprvé asi nebude nic názornějšího než náhled na obrázek s grafem (získaný ze serveru matematika.navajo.cz). Logaritmus je inverzní funkcí k funkci exponenciální. Pokud ve vztahu ay=x potřebujeme vypočítat hodnotu y, zjistíme ji takto: y=Loga x.
Šachový růst a logaritmická křivka
Nyní si musíme definovat, který aspekt naší šachové kariéry náleží které vlastnosti logaritmické funkce. Začněmě tím, že v grafu nás zajímá pouze ta část pro x>1, kdy funkce vstupuje do kladných hodnot. Také nás funkce bude zajímat pouze pro a>1 (pokud o logaritmech nic nevíte, pak na toto klidně zapomeňte, protože jiný na obrázku znázorněn není). Nyní už ale přejděme k definici hodnot x, y a a.
a = talent (platí nepřímá úměra, čím menší a, tím větší talent. Pokud a=2,718281828, pak je váš talent zcela přirozený )
)
x = práce (čas na trénink, jeho efektivita, energie, praxe, zkrátka vše, co musíte pro úspěch udělat)
y = kvalita hry (není v elo, o definici jednotky by se musel postarat nějaký expert z MFF, čím je však y vyšší, tím lépe hrajeme. Jak jsem již řekl, mým úkolem není vyřešit složitý problém a odpovědět na každý složitý dotaz, ale vytvořit problém podobný, jednoduchý a názorný.)
Co z toho všeho plyne?
Čím větší talent (menší a) máme, tím více při stejném úsilí (x) dosáhneme. To je celkem logické, na to asi nemusíte logaritmovat, abyste si to uvědomovali, že? Teď si ale řekneme něco mnohem důležitějšího. Nazval bych to zákonem snižování efektivity tréninku. Kdyby v šachu nebyl tento problém, stačilo by k jednoduché definici problematiky kariérního růstu použít funkci lineární.
Teď si ale řekneme něco mnohem důležitějšího. Nazval bych to zákonem snižování efektivity tréninku. Kdyby v šachu nebyl tento problém, stačilo by k jednoduché definici problematiky kariérního růstu použít funkci lineární.
Teď trochu odbočíme a ukážeme si případ, kdy náš zisk bude (přibližně) lineární, abyste pochopili rozdíl. Řekněme, že jste podnikatel a prodáváte brambory. Pokud vypěstujete 10 tun brambor, budete mít zisk r. Pokud vypěstujete 20 tun, váš zisk bude (samozřejmě trochu zjednodušeně) 2 r. To není žádné překvapení, proč by taky měla mít druhá polovina brambor nižší tržní hodnotu než ta první?
Šachy jsou ale jiné. Pokud neumíte hrát šachy (x=1), bude pro vás mít každá investovaná hodina obrovský význam a své nešachové přátele brzy předběhnete. Čím víc ale budete šachy umět, tím menší hodnotu budou jednotlivé znalosti mít a předběhnete s nimi čím dál menší počet soupeřů. (např. po prvních 100 hodinách tréninku předběhnete 9 000 000 lidí v ČR, po dalších 100 hodinách už ale předběhnete dalších třeba jen 500 000 hráčů. A až se dostanete ještě výš, budete pracovat týdny a měsíce na tom, abyste se posunuli jen o pár příček nahoru. A až se budete jmenovat David Navara, už nebudete mít koho předběhnout.) To je vysvětlení, proč jsem pro znázornění šachové kariéry vybral právě logaritmickou křivku. Když se na ni pořádně podíváme, ta má největší nárust z kraje (velké navýšení kvality hry y začátečníka za malé množství práce x). S nabývajícími hodnotami x (s pokračujícím studiem) jde y (kvalita naší hry) nahoru pomaleji a pomaleji.
Bod zlomu, úbytek motivace a důležitý faktor talentu
Jak je to krásné, když nárust y (kvality hry) je rychlejší než nárust x (práce). Pracujete málo a vidíte, jak za vámi odpadají konkurenti. Práce je v tuto chvili radost. Jak ale tušíte, toto nepůjde donekonečna a bude už jenom hůř. Bodem zlomu nazývám okamžik, kdy zisk na kvalitě hry začne být menší než oběť, kterou musíte přinést. Matematicky není obtížné tento bod popsat, jedná se o bod, ve kterém je derivace funkce rovna 1 (neboli tečna křivky v tomto bodě svírá 45° s osou x). Když vás ošidím o krátký výpočet, zjistíte, že množství práce, po kterém se dostanete do bodu zlomu spočítáte jako
x = 1/ln a
přičemž ln je logaritmus o základě e= 2,718281828. Tady končí radost a začíná dřina. Určitě stojí za zmínění, že čím větší talent máte (se snižujícím a), tím víc se prodlužuje doba, kdy to jde „samo“. A i po přelezení bodu zlomu bude úhel tečny ke grafu ještě dlouho poměrně vysoký (40°, pak 35° atd...). Naopak netalentovaní po přelezení bodu zlomu okamžitě končí s jakýmkoliv seriózním zlepšováním, tečna jejich funkce se totiž rychle stává skoro rovnoběžnou s osou x a tedy se zlepšují už jen symbolicky.
Status quo mezi stejně talentovanými hráči
Často slyším kolem sebe, že někteří hráči stagnují, že už jim to nejde nahoru, že na šachy asi kašlou atp. Nutnost stagnace ale vyplývá z grafu. To, že se jedná o samozřejmý matematický jev ale neznamená, že z úst některých lidí takové řeči nejsou myšleny spíše jako pomluva nebo urážka... Pokud jsou dva stejně talentovaní hráči ve stejnou chvíli stejně silní (mají stejná a, x i y), pak platí, že čím menší je derivace v bodě x (neboli čím menší je úhel mezi osou x a tečnou k funkci v bodě x, neboli čím menší je její směrnice k), tím víc se jeden nadře, aby toho druhého výrazně předběhl. Směrnici tečny funkce v bodě x vypočítáme opět s pomocí derivace.
k = 1/x/ln a
Nyní se zamyslete, jaké k by pro vás bylo ještě přijatelné, abyste pokračovali v seriózní práci? Pro rekreačního hráče to bude třeba pro k>1, neboli dokud nedosáhne bodu zlomu. Pro ambiciózního hráče pak třeba pro k>0,5, což znamená, že je ochoten za dvě pracovní jednotky dostat jen jednu odměnu. Pouze pár fanatiků bude pokračovat v práci, pokud k<0,1, což zanmená, že za 10 pracovních jednotek nebudou odměněni ani jednou celou odměnou.
Příklad: Není nepravděpodobné, že konstantě k (směrnici tečny ke grafu v bodě x) zatím ještě příliš nerozumíte. Představte si, že pro k=1 (bod zlomu) svého nepracujícího rivala se stejným talentem a stenou současnou výkoností předběhnete o 200 elo bodů na 1000 hodin práce. To není tak hrozné. Nyní si ale představte, že oba v práci pokročíte dál, po 2000 hodinách budete pořád na stejné úrovni (oba samozřejmě na výrazně vyšší). Pokud váš rival přestane s prací až teď a vy budete pokračovat, váš zisk proti němu na elo za 1000 hodin už nebude zdaleka 200 bodů, ale pouze k*200 bodů. A pokud už je vaše k pouze 0,1, stojí vám těch 20 elo bodů na 1000 hodin práce za to? A co když je vaše k ještě menší?
Jak již bylo řečeno, supertalenti mají v tomto určitou výhodu, protože s klesajícím a (rostoucím talentem) klesá k pomaleji a oni na sobě vidí pokroky déle než ti netalentovaní.
Máme tedy na to?
Až se příště budeme ptát, zdali na to máme (Já s Dejvem na titul GM, jiní na tituly IM, FM, nebo MS, elo 1900,...), měli bychom si tuto otázku položit trochu komplexněji. Máme dostatečně nízké a (velký talent), abychom nemuseli na náš cíl makat 150 let? Kolik x (pracovního nasazení) můžeme a chceme našemu cíli obětovat? Pokud si na tyto dvě otázky umíme odpovědět, pak už stačí jen odhadnout, zdali
loga x >= náš vytyčený cíl.
Děkuji za pozornost a omlouvám se těm, kteří se při podobné analýze spoléhají více na svou intuici než na vzorce a matematika prostě není jejich šálkem kávy. Intuice je zcela v pořádku a zde určitě i dostatečná, není ale na škodu zamyslet se občas i trochu jinak. Snažil jsem se logická fakta vysvětlovat hlavně slovně a matematiku uvádět pouze jako průvodní jev, jak se mi to ale povedlo, to musíte posoudit vy. Doufám, že v mém textu nebudete zase hledat gramatické chyby, na ty faktické ale budu zvědavý...
vkládání nových příspěvků bylo pozastaveno
příspěvky k článku
06.10.2011 14:47:06 | YF
dobrej clanek :)
05.03.2011 15:10:54 | Jozef
Mě se ten článeček líbí. Věděl jsem, že v šachu nedosahuji těch výsledků co bych chtěl a co lehce dosahují jiní. Článek má racionální jádro a při dostatečném nadhledu i dost věcí objasňuje. Navíc jsme si "zopákli" matiku  .
.
03.03.2011 12:32:35 | Tobi
to noELO: to máte pravdu, po sobě chyby zásadně nevidím. Takže jsem ráda za přátele, co mě na ně upozorní. Ale jinak si nemyslím, že bych svůj první příspěvek věnovala gramatice. Naopak - chyby, kterých jsem si v blogu všimla, jsem poslušně ignorovala. Takže bych to dál nerozebírala.
02.03.2011 21:32:32 | noELO
ad Tobi: když už jste věnovala většinu svého (nikoli Vašeho  ) - prvního příspěvku gramatice, neměla byste sama dělat chyby.
) - prvního příspěvku gramatice, neměla byste sama dělat chyby. 
Zdraví protivný korektor.
02.03.2011 18:32:06 | cicero
Štěpáne, gratuluji, že reagujete s nadhledem místo laciného hicování. Časem z Vás bude spokejeně ošlehaný b-logaritmik.
28.02.2011 19:36:06 | MM
Hmmm...Zrovna ty logaritmy děláme ve škole . Celou dobu si říkam proč se učíme takové zbytečnosti. Utíkám od učení na iternet...Dívám se a co spatřím Logaritmy! Krásná shoda okolnosti
. Celou dobu si říkam proč se učíme takové zbytečnosti. Utíkám od učení na iternet...Dívám se a co spatřím Logaritmy! Krásná shoda okolnosti  . Pěkný članek!
. Pěkný članek!
28.02.2011 14:24:43 | Štěpán
Pavel: Když je trénink i zábavou, to je paráda. Ale znám spoustu silných hráčů, kteří v životě nedrželi v ruce šachovou knihu, jejichž jediná příprava je ta před partií a kteří možná ani neumí dát mat koněm a střelcem...
Brambory: Nejsem žádný ekonom, v textu bylo PŘIBLIŽNĚ dvojnásobný, tím jsem se kryl proti všemožným faktorům, které neznám... Ale pokud mi chcete říct, že se ta křivka může tvarem byť jen blížit té logaritmické, asi vám věřit nebudu... Jaká tam bude odchylka od lineární funkce? Dle mého je to tak trochu srovnávání nesrovnatelného, ale mohu se plést...
Ale pokud mi chcete říct, že se ta křivka může tvarem byť jen blížit té logaritmické, asi vám věřit nebudu... Jaká tam bude odchylka od lineární funkce? Dle mého je to tak trochu srovnávání nesrovnatelného, ale mohu se plést...
Celý článek je pojmut nanejvýš abstraktně, když jsem řekl, že při k=1 získáte na 1000 hodin práce 200 elo bodů a že tedy při k=0.1 získáte na 1000 hodin práce 20 elo bodů, taky to nebyla úplně pravda, bylo to jen pro názornost. Zisk by byl samozřejmě menší než 20 bodů... k je derivací v jednom bodě, nikoli na celé 1000 hodinové části křivky... Šlo o co nejabstraktnější pojetí, se zanedbáním mnoha faktorů. Vždyť já ani neříkám, že naše kariéra má tvar log. křivky. Jen říkám, že je jí podobná...
Spatny matematik, liny clovek: Vzhledem k tomu, že jsem už na začátku deklaroval, že a, x, ani y nemá žádnou definovanou jednotku, chtěl byste po mně příliš... Toto je jen teoretické zamyšlení.
Honza Hučín: to zlepšení (databáze, trenér) se promítá na ose x, která není definována jako čas na šachy, ale jako čas * průměrná efektivita tréninku...
cicero: Ne každému se takový článek musí líbit...
28.02.2011 13:36:06 | Bond(James)
Naopak já dávám 3 palce nahoru, tedy ne že by mi to otevřelo oči (relativní snižování efektivity každé další hodiny strávené studiem musí být každému logicky uvažujícímu člověku jasné), ale čtivé to bylo.
Co se týče praktické aplikace vzorce, to si musí každý ohlídat sám - kolik jsem šachu věnoval hodin tréninku za poslední rok, o kolik mi stouplo ELO a z toho si vypočítám jaký mám talent a jaký je můj potenciál růstu.
A k tomu příkladu 2x více brambor = 2x více zisku - za stejné prodejní ceny by měl zisk být více než dvojnásobný, protože dojde k rozmělnění fixních nákladů, tam jde spíše o nasycení trhu a tím nutnému poklesu ceny a poklesu prodejnosti (třeba z 95% na 80%).
28.02.2011 11:41:50 | cicero
Lákavý pokus pro uspěšné uspávání dětí do 10 let aneb Nudně lze pojmout jakkoli vznešené téma. Autor demonstruje svou schopnost, jak zcela nezaujmout. Po šíleně dlouhé "minutě" se vypíná nebo přepíná a nikdo si nemůže stěžovat, že to má rozkoukané.
28.02.2011 11:29:43 | Honza Hučín
Vašek: Ovšem při produkci dvojnásobku není už druhý díl zatížen fixními náklady toho prvního...
Jinak je to jistě zajímavý článek a jen matematicky vyjadřuje, co většina z nás tak nějak cítí.
Jen bych ještě doplnil, že zejména rekreační šachista může náhle výkonnostně poskočit, když změní způsob tréninku, sežene si databázi partií, vypne hodnocení stroje při sledování online přenosu...
28.02.2011 10:36:56 | spatny matematik, liny clovek
Hezky den, zaujal me nadpis, ale jako liny clovek, ktery premysli, jen kdyz je donucen jsem precetl jen tak 3 odstavce.Dal uz jsem usoudil, ze bude nutno premyslet a to po narocnem vikendu....Mozna naivne jsem doufal, ze na konci bude nejaka "tabulka ci neco jineho, kam doplnim sve ELO, pocet hodin treninku (treba mesicne) hodnotu talentu (subjektivne by kazdy ohodnotil sam sebe 1-10) a par zaskrtavacich policek - trenujete s trenerem, ci trenujete vv klubu, mate konkurenci apod a jak dlouho chcete trenovat, resp. kolik let a nakonci bych zmackl tlacitko SPOCITAT a vyslo by mi elo, ktereho mohu dosahnout.
Takhle by se clanek libil me
28.02.2011 10:00:34 | Vašek
pěkný článek, souhlas, až na jednu zásadní věc - 2násobné tržby, neznamenají také 2násobný zisk (viz. příklad s pěstitelem brambor). Protože v šachovém příkladu abstrahujeme, abychom mohli najít nějaký obecný model, je nutné i v ekonomickém příkladu abstrahovat a potom jsou tedy vždy zisky nižší s dodatečně vytvořených výnosů než z těch minulých. Je tomu tak proto, že existuje zákon klesajících výnosů (zákon výroby vyjadřjící skutečnost, že při zvyšování jednoho vstupu, za podmínky nezměněných ostatních vstupů, dochází ke zpomalení růstu celkového produktu), zjednodušeně řečeno, budeme potřebovat další výrobní faktory (rozšířit výrobní halu, další stroje atd.), takže dodatečně vyrobené jednotky nám nepřinesou stejný zisk (další faktory nasycenost, trhu, zákon klesajícího mezního užitku pro spotřebitele atd. nechci zacházet do detailů). .... takže tyto axiomy, které věděl již třeba Samuelson (nositel Nobelovi ceny) nepíši pro nějaké poučování, ale proto, že vlastně šachy se vůbec neliší od našeho běžného života jak uvažujeme se svým rozpočtem, když jdeme na nákup, nebo jak uvažuje podnikatel, když něco vyrábí a snaží se to prodat, nebo jaké zákony platí i pro ostatní sporty. Každá dodatečná jednotka materiálu, úsilí, práce - jednoduše řečeno nákladů či výrobních faktorů nám přinese vždy menší přírůstek užitku než ta předchozí. A to je na tom to krásné, šachy jsou se všemi ostatními lidskými činnostmi v naprostém souladu.
27.02.2011 15:17:24 | Pavel
Hezký a zajímavý blog! Mám rád přesahy a náhledy ze zdánlivě nesouvisejících oblastí. Překvapilo mě to, zdánlivě nesamozřejmé, že čím větší talent, tím je dál bod zlomu, respektive tím křivka je i po bodu zlomu strmější... Je to logické, ale intuitivně bych býval hádal, že čím talentovanější jedinec, tím dříve se dostane k bodu, za kterým už leží jen stále více a více dřiny a méně a méně slasti.
A mimochodem: pro mě je šachový trénink potěšením! Včera jsem editoval texty knihy o mistru Opočenském, přehrával jeho partie s komentářem velmistra Horta, říkal jsem tomu šachový trénink (lecos jsem se tím učil) a hodně mě to bavilo. 
25.02.2011 20:36:16 | Tobi
...však ano, asi jsem do textu také měla vložit smajlíka pro odlehčení. Celá ta úvaha vyjádřená pomocí matematiky je určitě hodně zajímavá, dokonale originální pohled na věc.Líbí, líbí, líbí... 
25.02.2011 19:24:27 | Štěpán
Tobi: Tak na toto musím okamžitě reagovat, tento text nebyl ani v nejmenším určen k tomu, aby si někdo počítal, kdy má přestat hrát šachy Šachy ať každý hraje, dokud z toho má radost. Toto byla čistě matematicky pojatá úvaha o efektivitě TRÉNINKU ZA ÚČELEM ŠACHOVÉHO RŮSTU, kdy, jak třeba začínám na sobě pozorovat, se mé k dramaticky snížilo a s tím tak trochu opadla i motivace, kterou člověk měl, kdy to šlo po stovkách nahoru... Pokud někdo trénuje, protože z toho má radost, ať trénuje, jak se mu zachce. Pokud ale někdo například přemýšlí o dráze šachového (polo)profesionála, tento náhled na věc ho může v něčem obohatit. Ještě jednou, text neodrazuje od toho, co nás baví! Předpokládá naopak, že samotný trénink většinu z nás zas až tolik bavit nebude a podstupujeme ho spíše proto, že chceme vyhrávat ve hře, kterou máme rádi. Já jen poukazuji na teoretickou existenci hranice, kdy se nám místo tvrdé práce, za v ten moment už malou odměnu, vyplatí čas investovat jinde...
Šachy ať každý hraje, dokud z toho má radost. Toto byla čistě matematicky pojatá úvaha o efektivitě TRÉNINKU ZA ÚČELEM ŠACHOVÉHO RŮSTU, kdy, jak třeba začínám na sobě pozorovat, se mé k dramaticky snížilo a s tím tak trochu opadla i motivace, kterou člověk měl, kdy to šlo po stovkách nahoru... Pokud někdo trénuje, protože z toho má radost, ať trénuje, jak se mu zachce. Pokud ale někdo například přemýšlí o dráze šachového (polo)profesionála, tento náhled na věc ho může v něčem obohatit. Ještě jednou, text neodrazuje od toho, co nás baví! Předpokládá naopak, že samotný trénink většinu z nás zas až tolik bavit nebude a podstupujeme ho spíše proto, že chceme vyhrávat ve hře, kterou máme rádi. Já jen poukazuji na teoretickou existenci hranice, kdy se nám místo tvrdé práce, za v ten moment už malou odměnu, vyplatí čas investovat jinde...
K té gramatice, to bylo myšleno spíše s nadsázkou, přeci jen vzpomínky na kruté diktáty na střední mám ještě v živé paměti... A k té mé chytrosti, zas mě tak nepřeceňujte... Elo 2500 znamená jen to, že umím jakž takž hrát šachy...
A k té mé chytrosti, zas mě tak nepřeceňujte... Elo 2500 znamená jen to, že umím jakž takž hrát šachy...
25.02.2011 17:23:23 | Tobi
...jej, tak já jsem podle všeho měla šachy zabalit už dávno, jak jsem si právě spočítala. Kdepak matematika, ta by se ke slovu neměla vůbec pouštět! Super blog, který dal pořádně zabrat mým mozkovým závitům…škoda, že někdo tak chytrý, jako Vy, nedokáže nahlížet na korekci pravopisu a překlepů především jako na přínos pro Vás a Váš psaný projev, protože svou zmínkou „Doufám, že v mém textu nebudete zase hledat gramatické chyby…“ jste zcela jistě dosáhl toho, že si každý, kdo si případných chyb ve Vašich textech všimne, dvakrát rozmyslí Vás na ně upozornit a jinak většinou líbivé a zajímavé čtení, zůstane holt s chybami. A to je, myslím, trochu škoda.
starší články
- [23.11.2016]
Just another day at the office - [23.07.2016]
Tour de Pardubice - [25.08.2015]
Nabízím remis - [06.01.2013]
Druhé Vánoce - [06.12.2011]
Na dvou řadách aneb jeden nepřesný tah a je po partii - [22.08.2011]
Půlroční šachové vakuum a hned na to GM norma?! - [10.04.2011]
Koho si zvolíme příště? - [06.03.2011]
Příprava u výčepu aneb jak se hraje v extralize? - [25.02.2011]
Logaritmus v praxi aneb šachová kariéra z matematické perspektivy
- [16.01.2011]
Když se štěstí unaví aneb jak jsem vyhrál OPEN Praha
reserved by Pražská šachová společnost, o.s. | designed by pb | optimalized 1024x768 IE, FireFox